1. IEEE-754

자바스크립트는 [IEEE-754](https:// ko.wikipedia.org/wiki/IEEE_754)에 의거하여 정수와 부동소수점을 표기합니다.
IEEE-754 표기법 중 32BIT를 사용하는 단정도와 64BIT를 사용하는 배정도방식이 존재하는데
자바스크립트는 배정도 방식을 사용하여 정수와 부동소수점을 표기합니다.

2. 부호 비트 (SIGNED BIT)

자바스크립트는 배정도방식으로 저장하지만 실제로 개발자가 비트연산등을 수행하여 값을 저장할때에는 32BIT 정수로 변환하여 연산을 수행한 뒤 64BIT로 다시 변환하여 저장합니다.
0000 0000 0000 0000 0000 0000 0000 0000(2) 의 비트값이 존재한다고 했을때 첫 번째 비트를 부호 표현을 위한 비트로 따로 지정하게 되는데 이를 부호 비트라고 칭합니다.
부호비트는 0일때 양수를 1일때 음수를 나타냅니다.

3. 양수를 표현할때

먼저 정수를 저장하는 방법에 대해 알아보도록 하죠. 43이라는 값을 32비트로 저장하려면 먼저 2진수로 변환해야 합니다.
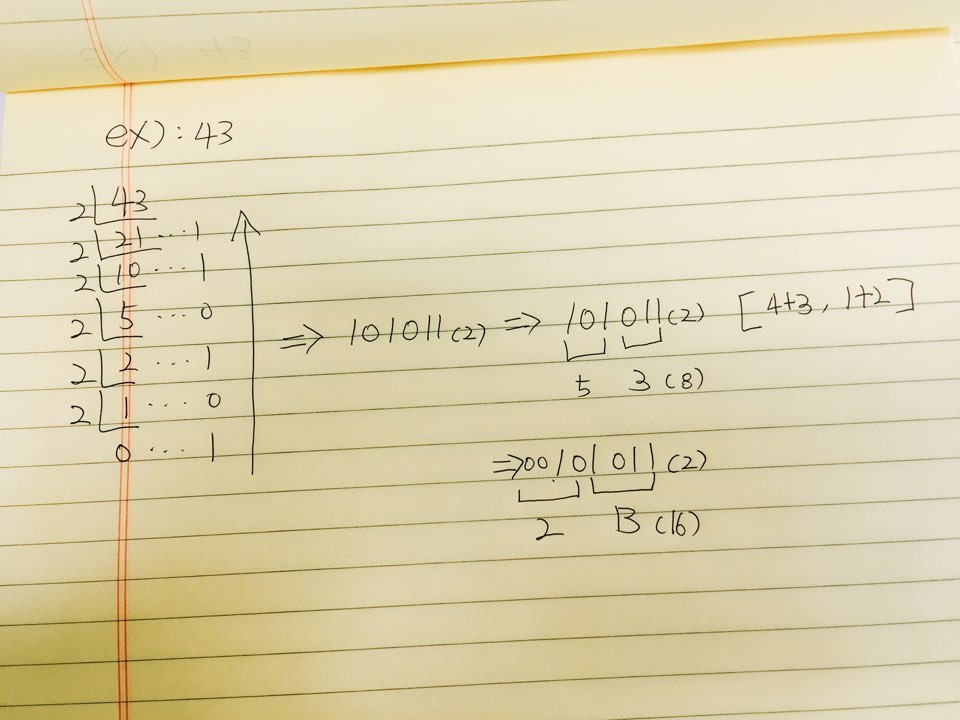이미지 이처럼 10진수 43을 2진수로 표현할 수 있고, 그를 8진수나 16진수등으로 변경할 수도 있습니다.
43이라는 정수값을 2진수로 변경하게 되면 101011(2)로 표기할 수 있고, 자바스크립트로 간단하게 사용하고자 한다면 toString을 사용하여 쉽게 구할 수도 있습니다.

var nubmer = 43..toString(2); // 101011

0000 0000 0000 0000 0000 0000 0010 1011(2) // 43(10)
0111 1111 1111 1111 1111 1111 1111 1111(2) // 2147483647(10)

따라서 10진수 43을 32비트로 저장할때에는 위와 같이 저장되며, 양수 표현에서 최대한으로 저장할 수 있는 값은 +2147483647입니다.

3. 음수를 표현할때

음수를 표현하는 방법은 여러가지 방법이 존재해왔습니다.

이미지

부호 절대값 방법(Sign Magnitude): 부호 비트를 제외한 수를 양수값으로 읽고, 부호비트에 따라 + - 를 인식하는 방법입니다. (이진수 계산이 되지 않기 때문에 컴퓨터에서 사용하지 않습니다.)

1의 보수방법(1's Complement): 양수값의 비트를 반전시켜서 음수를 표현하는 방법입니다. 0은 1로 1은 0으로 변환합니다. (-0과 +0인 경우가 존재하기 때문에 컴퓨터에서 사용하지 않습니다.)

2의 보수 방법(2's Complement): 1의 보수값에 +1을 한 값을 사용하며, -0이 없어지기 때문에 이 방법으로 음수를 표현합니다.

이처럼 2의 보수방법을 취하는 음수 표현법에 따라 -43이라는 값은 이처럼 변환되게 됩니다.

0000 0000 0000 0000 0000 0000 0010 1011(2) // 43(10)
1111 1111 1111 1111 1111 1111 1101 0100(2) // 43(10) 의 1의 보수
1111 1111 1111 1111 1111 1111 1101 0101(2) // 43(10) 의 2의 보수

또한 보수의 개념이므로 43의 2진수값과 43의 2의 보수값을 더하면 0이 되는 것을 볼 수 있습니다.
양수의 최대값으로 표현할 수 있는 값은 2147483647이고 이를 2진수로 표현하면
0111 1111 1111 1111 1111 1111 1111 1111(2) 이 됩니다.
하지만 음수는 양수보다 +1개만큼의 경우의 수를 더 포함하므로 음수로 표현할 수 있는 값은 2147483648이 됩니다.
이는 2진수로 표현하게 되면 1000 0000 0000 0000 0000 0000 0000 0000이 되는데요.

1000 0000 0000 0000 0000 0000 0000 0000(2) // 2147483648(10)
0111 1111 1111 1111 1111 1111 1111 1111(2) // 2147483648(10)의 1의 보수
1000 0000 0000 0000 0000 0000 0000 0000(2) // 2147483648(10)의 2의 보수

위처럼 계산이 되므로 음수 표현에서 최대한으로 저장할 수 있는 정수의 값은 -2147483648(10)가 됩니다.

4. 부동소수점 표기 방법

부동 소수 표현식 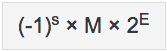이미지

s(Sign): 부호비트를 나타냅니다. (양수일때: 0, 음수일때: 1)
M(Mantissa): 가수부를 나타냅니다. (유효숫자)
E(Exponent): 지수부를 나타냅니다.

이미지

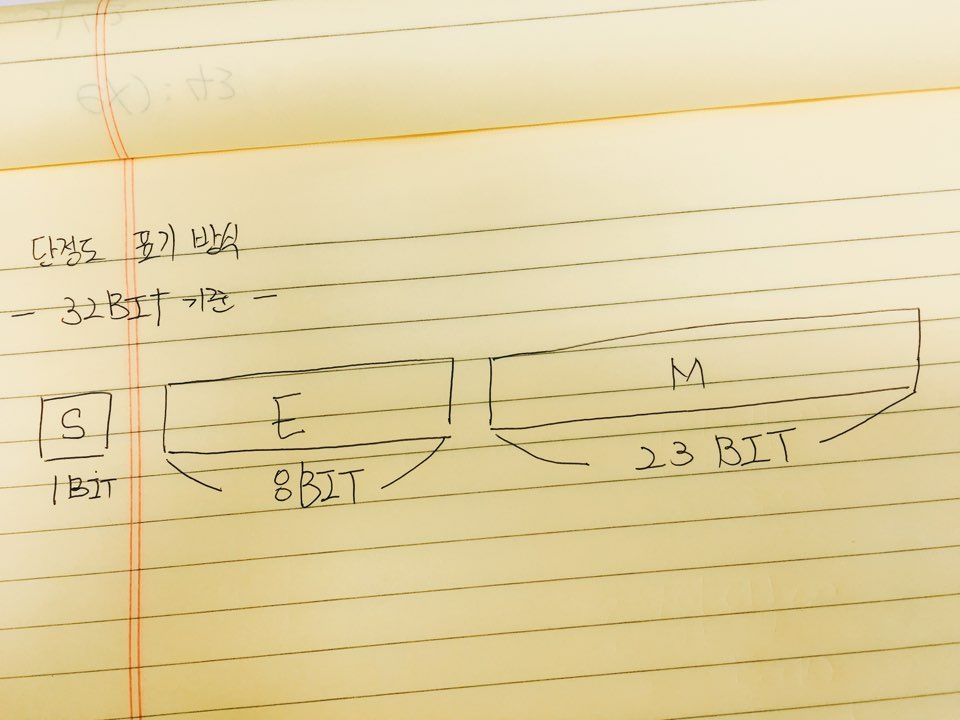
단정도 방식에서는 sign비트를 1비트로 Exponent를 8비트로 Mantissa를 23비트로 표현합니다.
배정도 방식에서는 sign비트를 1비트로 Exponent를 11비트로 Mantissa를 52비트로 표현합니다.

오늘은 43.6875라는 실수값이 어떻게 저장되는지에 대해 보도록 하겠습니다.

이미지

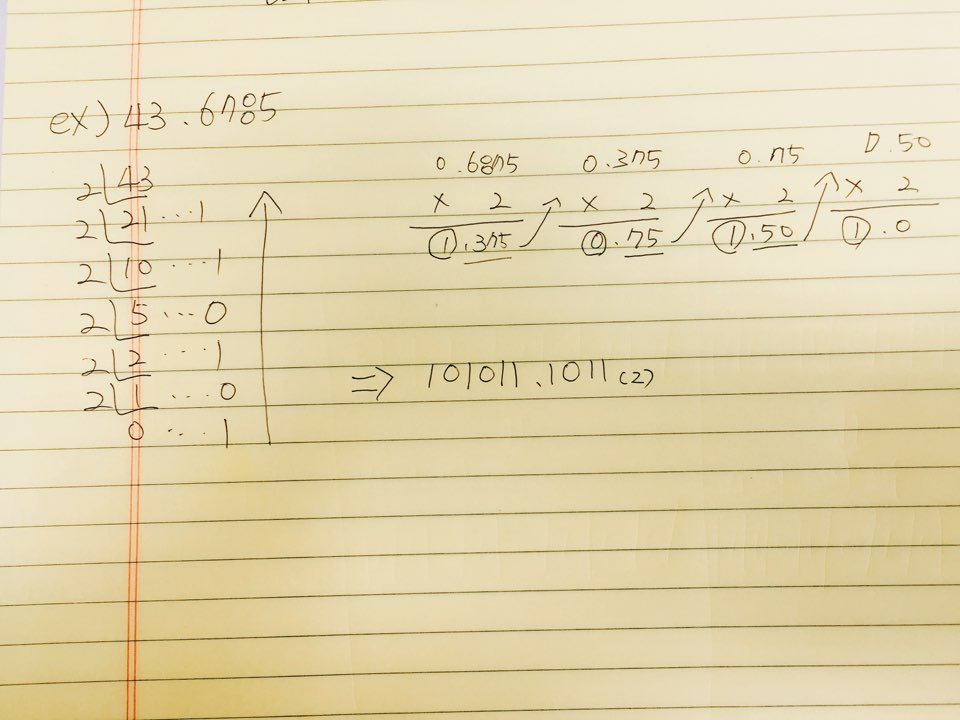
먼저 2진수로 변환하는 과정을 거쳐서 101011.1011(2)라는 값을 얻습니다.

Sign비트는 양수이므로 0이 됩니다.

Exponent를 구하기 위해 정규화 과정을 거칩니다.

이미지

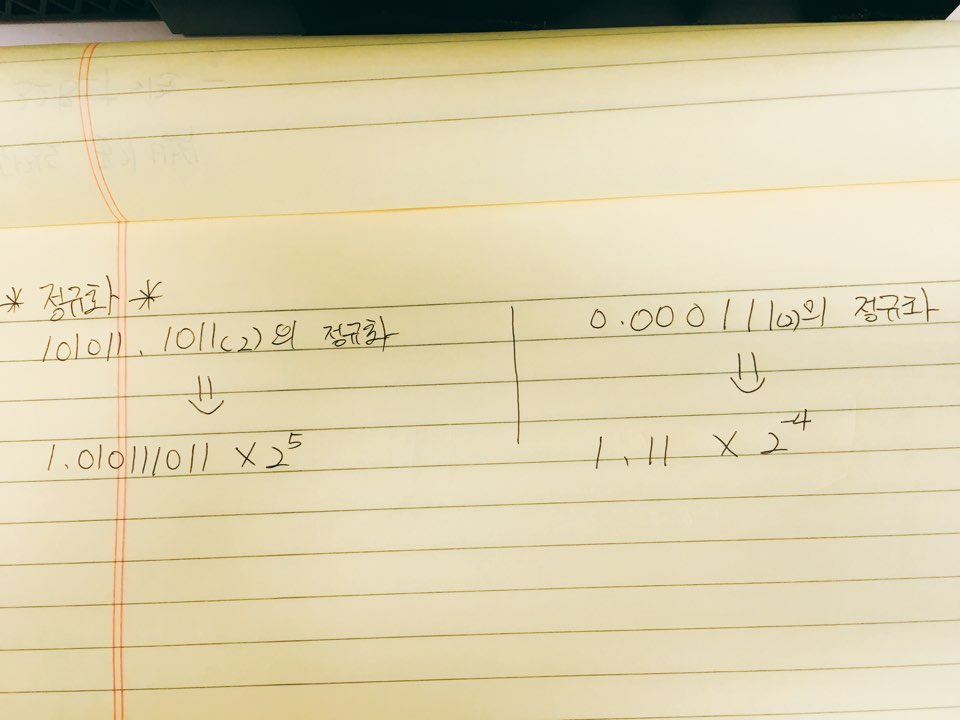
정규화란 2진수의 제일 왼쪽의 값이 1이 나오도록 소수점을 이동시키는 지수표현 방법을 말합니다.

정규화 과정을 마친 후 매직넘버를 구합니다.

이미지

매직넘버란 지수부에 음수가 들어가지 않게 하기위해 더해주는 수로서, 정규화되어진 지수의 값 5와 매직넘버 127을 더한 값 10진수 132를 구합니다.
그 후 해당 수를 2진수로 변환하여 얻은 값 10000100(2)를 Exponent에 저장합니다.

Mantissa를 구하기 위해, 정규화된 값을 다시 한번 참조 합니다.

43.6875(10)의 정규화된 값은 1.010111011 * (2 « 4) 입니다.

지수부는 저장을 완료 하였으므로 가수부의 값을 저장하면 되는데, 반드시 정규화된 결과값의 맨 첫번째 자리는 1이므로 조금이라도 많이 저장하기 위해 앞자리 1은 생략 합니다.

Mantissa는 0101 1101 1000 0000 0000 000가 되며

최종 결과값은 0 10000100 0101 1101 1000 0000 0000 000(2) 이 됩니다.

5. 0.1 + 0.2 !== 0.3

먼저 0.1을 2진수로 변환합니다.

0.1(10) => 0.0001100110011001100110011001100110011001100110011001100110011…….(2) 0.2(10) => 0.0011001100110011001100110011001100110011001100110011001100110…….(2)

그 후 정규화 과정을 거칩니다.

0.1(10) => 1.1001 1001 1001 1001 1001 1001………(2) * - (2 « 3) // 2의 -4승
0.2(10) => 1.1001 1001 1001 1001 1001 1001………(2) * - (2 « 2) // 2의 -3승

정규화 과정이 완료되면 위처럼 표기됩니다.

그럼 이를 부동소수점 표기방식으로 저장해보도록 할게요.

0.1의 저장

Sign은 양수이므로 0 입니다.
Exponent는 -4 + 127 = 123(10) => 1111011(2) 입니다. Mantissa는 맨앞의 1을 제외하고 저장하므로 1001 1001 1001 1001 1001 101입니다.

0.2의 저장

Sign은 양수이므로 0 입니다.
Exponent는 -3 + 127 = 124(10) => 1111100(2) 입니다. Mantissa는 맨앞의 1을 제외하고 저장하므로 1001 1001 1001 1001 1001 101입니다.

최종적으로 저장된 결과값
0.1 => 0 1111011 10011001100110011001101
0.2 => 0 1111100 10011001100110011001101

최종 결과는 이렇습니다. 하지만 여기서 눈여겨 보셔야 할 부분이 있는데요, 바로 가수부분이 23자리로 저장되면서 반올림되었다는 점입니다.

0.1과 0.2둘다 말이죠.

그러면 다시 0.1 + 0.2의 연산을 처리하기 위해, 해당 값을 가져와서 연산해 보도록 합시다.

0.1의 실수 변환

    // 0.1을 변환 
    // 먼저 가수부의 값을 가져와서 생략되어진 1을 추가합니다. 그리고 10진수로 변경합니다. 
    var mantissa = parseInt('1' + '10011001100110011001101', 2); // 13421773
    var exponent = -4;
    
    // 그리고, 1.10011001100110011001101 이 아닌
    // 110011001100110011001101을 연산했으므로 -23의 지수가 추가됩니다. 
    exponent += -23; 
    
    mantissa * Math.pow(2, exponent); 
    // 7.450580596923828e-9 그리고 두 개의 값을 곱해줍니다.  
    
    var result = mantissa * exponent; 
    // 0.10000000149011612 의 결과값이 보입니다.

0.2의 실수 변환

    // 0.2을 변환 
    // 먼저 가수부의 값을 가져와서 생략되어진 1을 추가합니다. 그리고 10진수로 변경합니다. 
    var mantissa = parseInt('1' + '10011001100110011001101', 2); // 13421773
    var exponent = -3;
    
    // 그리고, 1.10011001100110011001101 이 아닌
    // 110011001100110011001101을 연산했으므로 -23의 지수가 추가됩니다. 
    exponent += -23; 
    
    mantissa * Math.pow(2, exponent); 
    // 1.4901161193847656e-8 그리고 두 개의 값을 곱해줍니다.  
    
    var result = mantissa * exponent; 
    // 0.20000000298023224 의 결과값이 보입니다.

0.1 + 0.2 의 결과

    var number1 = 0.10000000149011612;
    var number2 = 0.20000000298023224; 
    
    console.log(number1 + number2); // 0.30000000447034836

대처방안

    var number1 = 0.10000000149011612;
    var number2 = 0.20000000298023224; 
    var result = (number1 + number2).toFixed(1);
    
    console.log(result); // 0.3

따라서, 0.1 + 0.2의 결과값은 다를 수 밖에 없습니다. 이를 유의하여 사용할때에는 소수점을 고정시키는 방법을 고려해야 합니다.

부동소수점 표현방식이었습니다.