수포자가 필요해서 정리하는 수학공식
DEGREE: 360도를 표현하며 60분법으로도 표현이 가능합니다.
우리가 일반적으로 사용하는 각도의 개념이라고 보면 됩니다.
그렇지만, 보통의 컴퓨터 프로그램들은 우리가 사용하는 DEGREE를 읽어 들여 계산하지 않고 RADIAN 이라는 값을 사용하여 계산하게 됩니다.
결국 호도법을 하게 된 이유는 RADIAN값을 구하기 위해서에요 !
그럼 한번 구해볼까요 ?

π(원주율): 원주율이란 원의둘레가 지름보다 몇배나 큰지를 나타난 비례값이에요. 그걸 공식으로 나타내본다면 π = 원의둘레 / 지름
이라는 결론이 나오겠지요.
그런데 우리는 이걸 알아둘 필요가 있어요. 1/3 == 3/9 //true 라는 것을요
그렇다는 이야기는 π = 반원의둘레 / 반지름 이기도 하다는 이야기가 되요.
호도법은 여기에서 시작 됩니다.
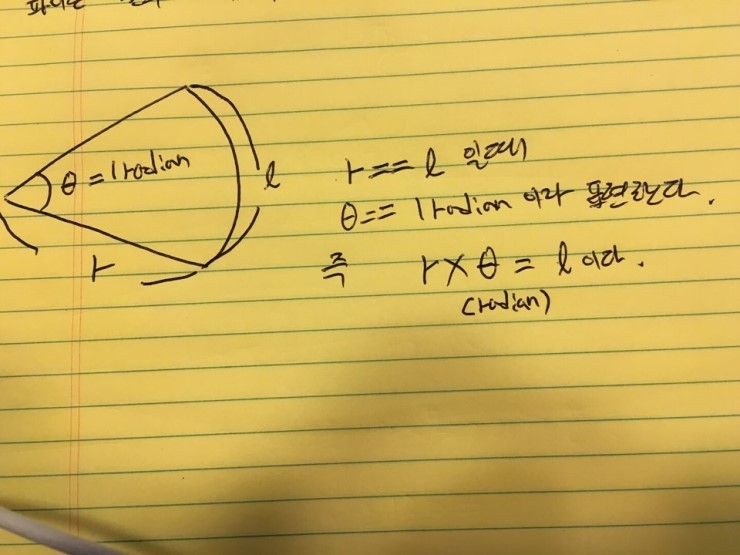
위의 그림을 보면 원뿔이 하나 있는데요, 반지름을 r이라고 하고 원뿔의 둘레를 l이라고 명명해요.
반지름 r과 l이 같을때 호안의 Θ(세타)를 1radian 이라고 부르기로 했어요.
이제 이 논리를 앞서 나왔던 π의 개념에 적용해볼까요 ?
π = 반원의둘레 / 반지름 일때 양변에 반지름을 곱해주면 이런 결과가 나옵니다.
π * 반지름 = 반원의 둘레 라는 공식이 되요.
이로써 우리는 위의 공식과 합칠 수 있게 되었습니다
Θ * r = l 이 되는것이죠. 이걸 꼭 기억하셔야 합니다.
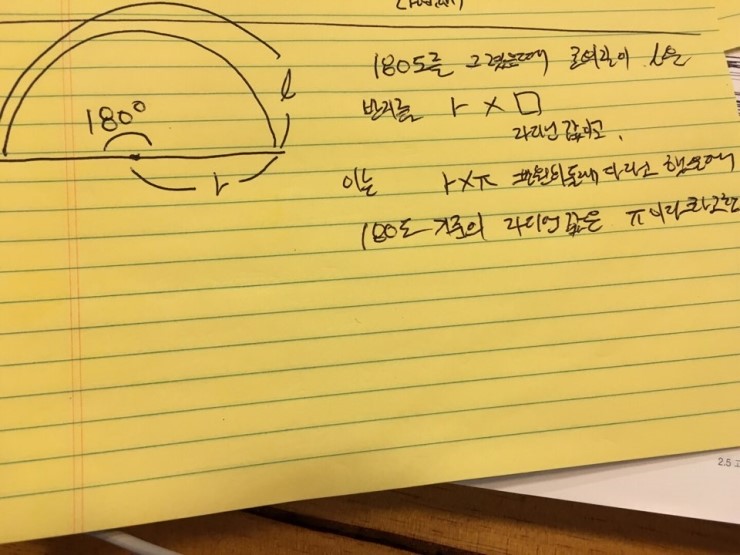
그리고 위 이미지를 볼까요 ? 거의 다 왔습니다. :)
우리는 호도법을 공부하면서 라디안값이 어떻게 구해지는지에 대해서 배웠고
Θ * r = l
위와 같은 공식을 얻어낼 수 있었지요 ?
그러면 반원의 기준으로 돌아와서 다시 한번 생각해 보시면 180(degree)일때의 반지름과 반원의 둘레를 생각해보자구요.
결국 이건 Θ(180deg) * r(반지름) = l(반원의길이) 와 같게 됩니다.
다시 맨 처음으로 돌아가볼까요 ??
π = 반원의둘레 / 반지름 이었지요 ?
이를 해 보았더니 π * 반지름 = 반원의 둘레 이렇게 되었지요 ?
결국은 180(deg)일때 π = 180(deg)의 Θ(세타) 값이 됩니다.
π는 180도의 radian값이 된다는 이야기입니다.
그럼 최종적으로 정리해볼까요 ?
`` π = 180(deg)의 Θ(세타) 값이다.`
특정 DEGREE를 입력받았을때 그 DEGREE의 RADIAN값을 구하는 방법은 다음과 같습니다.
const deg = 180;
const rad = Math.PI / 180 * deg;
즉 π를 180으로 나누면 1deg에 대한 radian값이 구해지죠. 그럼 내가 원래 구하고자했던 degree만큼 곱해주면 되는거죠 !
그럼 RADIAN값을 DEGREE로 바꾸는 방법은 어떻게 될까요 ?
역산 하면 됩니다. :)
양변에 180 / Math.PI를 곱해주면 되겠지요 ?!
const rad = 90;
const deg = 180 / Math.PI * deg;
이로써 호도법 및 RADIAN에 대한 정리를 마칩니다.
